函数
void	csky_biquad_cas_df1_32x64_init_q31 (csky_biquad_cas_df1_32x64_ins_q31 S, uint8_t numStages, q31_t pCoeffs, q63_t *pState, uint8_t postShift)

void	csky_biquad_cas_df1_32x64_q31 (const csky_biquad_cas_df1_32x64_ins_q31 S, q31_t pSrc, q31_t *pDst, uint32_t blockSize)

简要说明

这个函数为Q31数据类型实现了一个高精度二阶级联滤波器。滤波器的系数系数是1.31格式，状态变量是1.63格式。双精度状态变量减少滤波器中的量化噪声，并提供了更清晰的输出。这些滤波器函数在实现奇点接近单位圆的滤波器时很有用。常见于截至频率很低的低通或者高通滤波器。

函数以块为单位操作输入输出数据，每次调用函数处理 blockSize 个样本. pSrc 和 pDst 指向输入和输出数组，包含 blockSize 个Q31数.

算法

每个二阶阶段使用差分方程实现二阶滤波:

    y[n] = b0 * x[n] + b1 * x[n-1] + b2 * x[n-2] + a1 * y[n-1] + a2 * y[n-2]

一个直接I型算法的每个阶段使用5个系数和4个状态变量。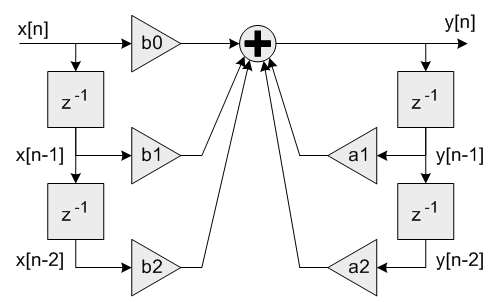

单个二阶滤波器阶段

系数 b0, b1, 和 b2 与输入信号 x[n] 相乘，并且被称为前馈系数。系数 a1 和 a2 与输出信号 y[n] 相乘，并且被称为反馈系数。

需要注意反馈系数的符号。有些设计工具使用差分方程：

    y[n] = b0 * x[n] + b1 * x[n-1] + b2 * x[n-2] - a1 * y[n-1] - a2 * y[n-2]

这种情况下，反馈系数a1 和 a2 在使用CSI DSP库的时候，必须取反。

: 高阶滤波器通过级联的二阶单元实现。 numStages 指定使用了多少二阶阶段。比如，第8阶滤波器是numStages=4 的二阶阶段。

使用二阶级联的8阶滤波器
第9阶滤波器可以看做numStages=5 的二阶阶段，系数配置为第一阶(b2=0 和 a2=0).

pState 指向状态变量数组. 每个二阶阶段有4个状态变量x[n-1], x[n-2], y[n-1], 和 y[n-2] ，并且为了提高精度，每个状态变量都是1.63格式. 状态变量在数组中的排列:

    {x[n-1], x[n-2], y[n-1], y[n-2]}

: 阶段1使用最开始的4个状态变量，阶段2使用接下来的4个状态变量，依次类推。状态变量数组总共有4*numStages 个1.63格式的值。每个块数据处理会更新状态变量，不会更新系数。

初始化函数

初始化函数处理以下操作：

设置数据结构字段的值.
清零状态buffer的值. 不使用初始化函数，手动处理这些操作，需要设置结构体实例内的以下字段： numStages, pCoeffs, postShift, pState. 将pState的所有值置0。

是否使用初始化函数是可选的. 但是，如果使用初始化函数，则结构体实例不能被放在常量数据段。想要将结构体实例放在常量数据段，则必须手动的初始化结构体实例。在静态初始化之前，先把状态buffer中的值置0。比如，静态的初始化滤波器结构实例使用：

    csky_biquad_cas_df1_32x64_ins_q31 S1 = {numStages, pState, pCoeffs, postShift};

其中 numStages 是滤波器中二阶阶段的数量; pState 是状态buffer的地址; pCoeffs 是系数buffer的地址; postShift 是移位数。

定点行为

使用32x64的二阶级联滤波函数需要多加注意。需要考虑以下问题:

滤波器系数表示为小数值，并且系数限制在[-1 +1) 范围之间. 处理函数有一个额外的缩放参数 postShift 用于给滤波器系数放大到超过[+1 -1) . 滤波器的累加器的输出是一个移位寄存器，结果移动postShift 位.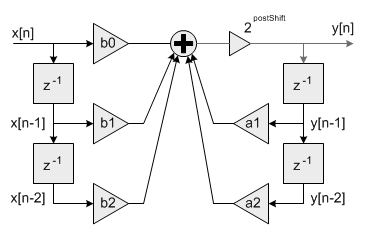

定点二阶累加后带移位

这本质上将滤波器的系数缩放了 2^postShift. 比如，为了表示系数

   {1.5, -0.8, 1.2, 1.6, -0.9}

可以设置pCoeffs数组为:

   {0.75, -0.4, 0.6, 0.8, -0.45}

并且设置postShift=1

: 第二个要注意的事情是滤波器的增益. 二阶滤波器的频率响应是它函数的一个系数。通过滤波器的增益可能超过1.0，这意味着滤波器增加了某些频率的幅度。这意味着幅度小于1.0的输入信号可能导致输出大于 1.0，因此基于滤波器的实现，这些信号可能会饱和或溢出。为了避免这种行为，滤波器需要按比例缩小，使得其峰值增益小于1.0，或输入信号必须按比例缩小，以便输入和滤波器的组合不会溢出。

函数说明

void csky_biquad_cas_df1_32x64_init_q31	(	csky_biquad_cas_df1_32x64_ins_q31 *	S,
		uint8_t	numStages,
		q31_t *	pCoeffs,
		q63_t *	pState,
		uint8_t	postShift
	)

参数

系数和状态顺序:

系数按以下顺序保存在数组pCoeffs :

    {b10, b11, b12, a11, a12, b20, b21, b22, a21, a22, ...}

其中 b1x 和 a1x 是第一个阶段的系数， b2x 和 a2x 是第二个阶段的系数，依次类推。 pCoeffs 数组总共有5*numStages个数值.

pState 是指向状态数组的指针，每个状态变量都是1.63的格式. 每个二阶阶段有4个状态变量 x[n-1], x[n-2], y[n-1], 和y[n-2]. 状态变量排列在数组的顺序如下:

    {x[n-1], x[n-2], y[n-1], y[n-2]}

最前面是第一阶段的4个状态变量, 然后是第二阶段的4个状态变量，依次类推。状态数组总共有4*numStages 个数值. 状态变量在数据块处理之后更新，系数不会更新。

void csky_biquad_cas_df1_32x64_q31	(	const csky_biquad_cas_df1_32x64_ins_q31 *	S,
		q31_t *	pSrc,
		q31_t *	pDst,
		uint32_t	blockSize
	)

参数

: 函数实现使用了一个内部64位累加器。累加器的用的是2.62格式，维持了中间乘法结果全精度，但是只有1个保护位。因此，如果累加器结果溢出，会往符号位覆盖，而不是截断。为了防止溢出，输入信号必须先缩小两个位，到[-0.25 +0.25)范围. 5个相乘结果相加后，2.62累加器移动postShift位，并且结果通过丢弃低32位，截断为1.31格式。

: CSI DSP库提供两个相关的函数。 csky_biquad_cascade_df1_q31() 用32位的系数和状态变量，以及Q63累加器实现二阶级联。 csky_biquad_cascade_df1_fast_q31() 用32位的系数和状态变量，以及Q31累加器实现二阶级联。