函数
void	csky_fir_f32 (const csky_fir_instance_f32 S, float32_t pSrc, float32_t *pDst, uint32_t blockSize)
	浮点FIR滤波器处理函数更多...

void	csky_fir_fast_q15 (const csky_fir_instance_q15 S, q15_t pSrc, q15_t *pDst, uint32_t blockSize)

void	csky_fir_fast_q31 (const csky_fir_instance_q31 S, q31_t pSrc, q31_t *pDst, uint32_t blockSize)

void	csky_fir_init_f32 (csky_fir_instance_f32 S, uint16_t numTaps, float32_t pCoeffs, float32_t *pState, uint32_t blockSize)

csky_status	csky_fir_init_q15 (csky_fir_instance_q15 S, uint16_t numTaps, q15_t pCoeffs, q15_t *pState, uint32_t blockSize)

void	csky_fir_init_q31 (csky_fir_instance_q31 S, uint16_t numTaps, q31_t pCoeffs, q31_t *pState, uint32_t blockSize)

void	csky_fir_init_q7 (csky_fir_instance_q7 S, uint16_t numTaps, q7_t pCoeffs, q7_t *pState, uint32_t blockSize)

void	csky_fir_q15 (const csky_fir_instance_q15 S, q15_t pSrc, q15_t *pDst, uint32_t blockSize)
	Q15 FIR滤波器的处理函数更多...

void	csky_fir_q31 (const csky_fir_instance_q31 S, q31_t pSrc, q31_t *pDst, uint32_t blockSize)

void	csky_fir_q7 (const csky_fir_instance_q7 S, q7_t pSrc, q7_t *pDst, uint32_t blockSize)

简要说明

这些函数实现了Q7，Q15，Q31和浮点数据类型的的有限冲激响应（FIR）滤波器，还有Q15和Q31的快速版本。还是以块为单位处理输入输出数据，每次调用滤波器函数处理 blockSize 个样本. pSrc 和 pDst 指向输入和输出数组，数组有 blockSize 个值.

算法:

FIR滤波器的算法建立在一系列的乘加（MAC）操作之上。每个滤波器系数 b[n] 和一个状态变量相乘，状态变量与之前的输入样本 x[n] 相同.

     y[n] = b[0] * x[n] + b[1] * x[n-1] + b[2] * x[n-2] + ...+ b[numTaps-1] * x[n-numTaps+1]

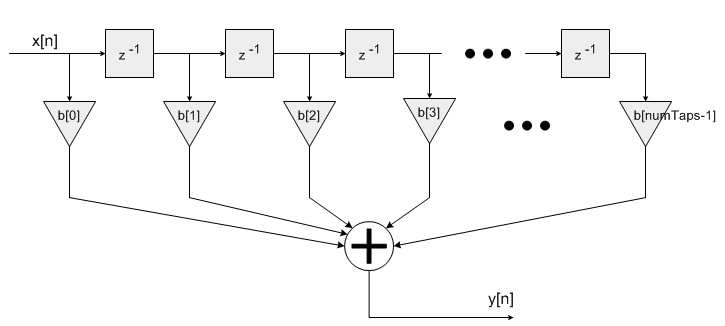
: 有限冲激响应滤波器

: pCoeffs 指向系数数组，数组的大小是 numTaps. 系数按以下顺序保存：

     {b[numTaps-1], b[numTaps-2], b[N-2], ..., b[1], b[0]}

: pState 指向状态数组，数组的大小是 numTaps + blockSize - 1. 状态数组的样本保存顺序如下：

     {x[n-numTaps+1], x[n-numTaps], x[n-numTaps-1], x[n-numTaps-2]....x[0], x[1], ..., x[blockSize-1]}

: 注意：状态缓存的长度超过了系数数组的长度 blockSize-1. 扩展之后的状态缓存长度，可以避免循环寻址，并且显著提升速度。循环寻址是用在传统FIR滤波器的一种寻址方式。状态变量在每块数据操作之后更新，系数不更新。

结构体实例: 滤波器的系数和状态变量都保存在数据结构的实例中。每个滤波器都必须有一个单独的结构体实例。系数数组可能可以在几个实例之间共享，但是状态变量数组不能共享。为支持的4种数据类型分别提供了不同的结构体实例声明。

初始化函数

为每种支持的数据类型都提供了一个相应的初始化函数。初始化函数处理以下操作：

设置内部结构体字段的值
清零状态缓存中的值如果手动初始化，而不调用初始化函数，需要指定结构体实例的以下字段： numTaps, pCoeffs, pState. pState中的所有值置0.

是否使用初始化函数是可选的。但是，使用了初始化函数，则不能将结构体实例放在常量数据段。要将结构体实例放在常量数据段，则必须手动初始化结构体实例。在静态初始化之前，要确保状态缓存中的值已经清零。下面的代码，为4种不同的滤波器，静态的初始化了结构体实例。

*csky_fir_instance_f32 S = {numTaps, pState, pCoeffs};
*csky_fir_instance_q31 S = {numTaps, pState, pCoeffs};
*csky_fir_instance_q15 S = {numTaps, pState, pCoeffs};
*csky_fir_instance_q7 S =  {numTaps, pState, pCoeffs};

其中 numTaps 是滤波器中的系数数量; pState 是状态缓存的地址; pCoeffs 是系数缓存的地址

定点行为: 使用定点FIR滤波器函数需要注意。特别是要考虑，在每个函数内使用的累加器的溢出和饱和行为。具体参考每个函数各自的文档和使用说明。

函数说明

void csky_fir_f32	(	const csky_fir_instance_f32 *	S,
		float32_t *	pSrc,
		float32_t *	pDst,
		uint32_t	blockSize
	)

参数

[in]	*S	指向浮点FIR滤波器结构体实例
[in]	*pSrc	指向输入数据块
[out]	*pDst	指向输出数据块
[in]	blockSize	输入样本的数量

返回: none.

示例:: csky_fir_example_f32.c , 以及 csky_signal_converge_example_f32.c.

void csky_fir_fast_q15	(	const csky_fir_instance_q15 *	S,
		q15_t *	pSrc,
		q15_t *	pDst,
		uint32_t	blockSize
	)

参数

[in]	*S	指向Q15 FIR滤波器结构体实例
[in]	*pSrc	指向输入数据块
[out]	*pDst	指向输出数据块
[in]	blockSize	输入样本的数量

返回: none.

缩放和溢出行为:

: 这个快速版本使用一个2.30格式的32位累加器。累加器维持了中间乘法的所有精度，但是只有一个保护位。因此为了防止溢出，输入信号必须缩小 log2(numTaps) 位. 最后2.30 格式累加器截断为 2.15 格式，并且饱和为 1.15 格式.

: 函数 csky_fir_q15() 是这个函数的一个慢速版本，使用了一个64位累加器，防止溢出。慢速和快速版本使用了相同的结构体实例。可以使用函数 csky_fir_init_q15() 初始化滤波器结构体。

void csky_fir_fast_q31	(	const csky_fir_instance_q31 *	S,
		q31_t *	pSrc,
		q31_t *	pDst,
		uint32_t	blockSize
	)

参数

[in]	*S	指向Q31结构体实例
[in]	*pSrc	指向输入数据块
[out]	*pDst	指向输出数据块
[in]	blockSize	处理的样本数量

返回: none.

缩放和溢出行为:

: 函数为了优化速度，舍弃了一些定点精度和溢出保护。每个 1.31 和 1.31 相乘的结果截断为 2.30 格式. 这些中间结果在一个2.30格式累加器相加。最后，累加器饱和转换为1.31的结果。快速版本和标准版本有一样的溢出行为，因为丢弃了每次相乘结果的低32位，所以相对提供了更少的精度。为了防止溢出，输入信号必须缩小 log2(numTaps) 个位.

: 函数 csky_fir_q31() 是这个函数的一个慢速版本，使用了一个64位累加器，提供了更高的精度。慢速和快速版本使用了相同的结构体实例。可以使用函数 csky_fir_init_q31() 初始化滤波器的结构体.

void csky_fir_init_f32	(	csky_fir_instance_f32 *	S,
		uint16_t	numTaps,
		float32_t *	pCoeffs,
		float32_t *	pState,
		uint32_t	blockSize
	)

参数

[in,out]	*S	指向浮点FIR滤波器结构体实例
[in]	numTaps	滤波器内系数数量
[in]	*pCoeffs	指向滤波器系数缓存
[in]	*pState	指向状态缓存
[in]	blockSize	处理的样本数量

返回: none.

描述说明:

pCoeffs 指向滤波器系数数组，保存的顺序如下：

   {b[numTaps-1], b[numTaps-2], b[N-2], ..., b[1], b[0]}

: pState 指向状态变量的数组。 pState 是长度为 numTaps+blockSize-1 的样本, 其中 blockSize 是传递给 csky_fir_f32() 的输入样本数量.

示例:: csky_fir_example_f32.c , 以及 csky_signal_converge_example_f32.c.

csky_status csky_fir_init_q15	(	csky_fir_instance_q15 *	S,
		uint16_t	numTaps,
		q15_t *	pCoeffs,
		q15_t *	pState,
		uint32_t	blockSize
	)

参数

[in,out]	*S	指向Q15 FIR滤波器结构体实例
[in]	numTaps	滤波器的系数数量，必须是偶数，并且大于等于4。
[in]	*pCoeffs	指向滤波器系数缓存
[in]	*pState	指向状态缓存
[in]	blockSize	处理样本的数量

返回: 初始化成功则函数返回 CSKY_MATH_SUCCESS ，如果numTaps小于4或者不是偶数，则返回 CSKY_MATH_ARGUMENT_ERROR 。

描述说明:

pCoeffs 指向滤波器系数数组，系数保存的顺序如下：

   {b[numTaps-1], b[numTaps-2], b[N-2], ..., b[1], b[0]}

注意： numTaps 必须是偶数，并且大于等于4。实现奇数长度的滤波器，则将 numTaps 加1，然后将最后的系数设成0。比如，要实现一个滤波器的 numTaps=3 ，系数是：

    {0.3, -0.8, 0.3}

改成 numTaps=4 ，使用系数：

    {0.3, -0.8, 0.3, 0}.

类似的，实现只有两个点的滤波器

    {0.3, -0.3}

改成 numTaps=4 ，使用系数：

    {0.3, -0.3, 0, 0}.

: pState 指向状态变量的数组。 pState 的长度是 numTaps+blockSize, 其中 blockSize 作为输入样本的数量传给 csky_fir_q15().

void csky_fir_init_q31	(	csky_fir_instance_q31 *	S,
		uint16_t	numTaps,
		q31_t *	pCoeffs,
		q31_t *	pState,
		uint32_t	blockSize
	)

参数

[in,out]	*S	指向Q31 FIR滤波器结构体实例
[in]	numTaps	滤波器中的系数数量
[in]	*pCoeffs	指向滤波器系数缓存
[in]	*pState	指向状态缓存
[in]	blockSize	处理的样本数量

返回: none.

描述说明:

pCoeffs 指向滤波器系数数组，系数保存的顺序如下：

   {b[numTaps-1], b[numTaps-2], b[N-2], ..., b[1], b[0]}

: pState 指向状态变量的数组。 pState 的长度是 numTaps+blockSize-1 , 其中 blockSize 作为输入样本的数量传入 csky_fir_q31().

void csky_fir_init_q7	(	csky_fir_instance_q7 *	S,
		uint16_t	numTaps,
		q7_t *	pCoeffs,
		q7_t *	pState,
		uint32_t	blockSize
	)

参数

[in,out]	*S	指向Q7 FIR滤波器结构体实例
[in]	numTaps	滤波器中的系数数量
[in]	*pCoeffs	指向滤波器系数缓存
[in]	*pState	指向状态缓存
[in]	blockSize	处理的样本数量

返回: none

描述说明:

pCoeffs 指向滤波器系数数组，系数保存的顺序如下：

   {b[numTaps-1], b[numTaps-2], b[N-2], ..., b[1], b[0]}

: pState 指向状态变量的数组。 pState 的长度是 numTaps+blockSize-1 , 其中 blockSize 作为输入样本的数量传入 csky_fir_q7().

void csky_fir_q15	(	const csky_fir_instance_q15 *	S,
		q15_t *	pSrc,
		q15_t *	pDst,
		uint32_t	blockSize
	)

参数

[in]	*S	指向Q15 FIR结构体实例
[in]	*pSrc	指向输入数据块
[out]	*pDst	指向输出数据块
[in]	blockSize	处理样本的数量

返回: none.

限制: 如果芯片不支持分对齐访问，则定义宏 UNALIGNED_SUPPORT_DISABLE 同时，输入，输出，临时buffer，都应该是32位对齐。

缩放和溢出行为:

: 函数实现使用了一个内部64位累加器。输入都是1.15格式的，乘法生成2.30结果。 2.30格式的中间结果在34.30格式的64位累加器累加。由于有33个保护位，所以不会有溢出风险。 34.30的结果丢弃低15位截断为34.15格式，然后饱和成为1.15格式的结果。

: 函数 csky_fir_fast_q15() 是这个函数的一个快速版本，但是丢失了更多的精度

void csky_fir_q31	(	const csky_fir_instance_q31 *	S,
		q31_t *	pSrc,
		q31_t *	pDst,
		uint32_t	blockSize
	)

参数

[in]	*S	指向Q31 FIR结构体实例
[in]	*pSrc	指向输入数据块
[out]	*pDst	指向输出数据块
[in]	blockSize	处理样本的数量

返回: none.

缩放和溢出行为:

: 函数实现使用了一个内部64位累加器。输入数据表示为1.31格式。中间乘法生成2.62格式的结果，结果在2.62格式的64位累加器累加。因为只有一个保护位，所以需要缩小输入信号来防止溢出。需要缩小log2(numTaps)才可以保证没有溢出。最后，2.62格式右移31位，然后饱和生成1.15格式的结果。

: 函数 csky_fir_fast_q31() 是这个函数的一个快速版本，但是丢失了更多的精度

void csky_fir_q7	(	const csky_fir_instance_q7 *	S,
		q7_t *	pSrc,
		q7_t *	pDst,
		uint32_t	blockSize
	)

参数

[in]	*S	指向Q15 FIR结构体实例
[in]	*pSrc	指向输入数据块
[out]	*pDst	指向输出数据块
[in]	blockSize	处理样本的数量

返回: none.

缩放和溢出行为:

: 函数实现使用了一个内部32位累加器。输入都是1.7格式，相乘的结果是2.14格式。 2.14格式的结果在18.14格式的32位累加器中累加。中间结果不会有溢出风险，而且可以保留所有的精度。 18.14 的结果丢弃低7位，截断为18.7格式，最后饱和为1.7格式。