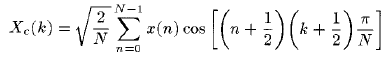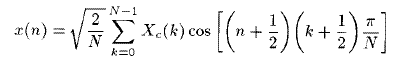|
| void | csky_dct4_f32 (const csky_dct4_instance_f32 *S, float32_t *pState, float32_t *pInlineBuffer) |
| | 浮点DCT4/IDCT4处理函数 更多...
|
| |
| csky_status | csky_dct4_init_f32 (csky_dct4_instance_f32 *S, csky_rfft_instance_f32 *S_RFFT, csky_cfft_radix4_instance_f32 *S_CFFT, uint16_t N, uint16_t Nby2, float32_t normalize) |
| | 浮点 DCT4/IDCT4 初始化函数. 更多...
|
| |
| csky_status | csky_dct4_init_q15 (csky_dct4_instance_q15 *S, csky_rfft_instance_q15 *S_RFFT, csky_cfft_radix4_instance_q15 *S_CFFT, uint16_t N, uint16_t Nby2, q15_t normalize) |
| | Q15 DCT4/IDCT4初始化函数 更多...
|
| |
| csky_status | csky_dct4_init_q31 (csky_dct4_instance_q31 *S, csky_rfft_instance_q31 *S_RFFT, csky_cfft_radix4_instance_q31 *S_CFFT, uint16_t N, uint16_t Nby2, q31_t normalize) |
| | Q31 DCT4/IDCT4 初始化函数 更多...
|
| |
| void | csky_dct4_q15 (const csky_dct4_instance_q15 *S, q15_t *pState, q15_t *pInlineBuffer) |
| | Q15 DCT4/IDCT4处理函数 更多...
|
| |
| void | csky_dct4_q31 (const csky_dct4_instance_q31 *S, q31_t *pState, q31_t *pInlineBuffer) |
| | Q31 DCT4/IDCT4处理函数 更多...
|
| |
离散余弦变换 (DCT) 可以用来构建出能量集中在光谱较低部分的输出。意味着可以用最小的数值来表示信号,在存储和传输中都很有用。因此广泛应用在信号和图片编码程序中。 DCT系列 (DCT 类型- 1,2,3,4) 是均匀边界条件的不同组合结果。 DCT系列有出色的能量包装特性,特别是在数据压缩方面。
DCT本质上是一个实数信号偶扩展的离散傅里叶变换(DFT)。 输入数据的重新排序可以让计算DCT变成计算一个实数信号的DFT,以及少量的附加操作。 因此特定硬件和软件就可以按照DFT实现一个简单有效的DCT算法。
DCT2型的内部可以用快速傅里叶变换(FFT)实现,由于变换应用在实数数值,因此可以使用实数FFT算法。 DCT4 的实现则使用了 DCT2,因为他们的实现很相似,只差了一些预处理和后期处理。 DCT2 的实现可以描述为以下步骤:
- 输入重排序
- 计算实数FFT
- 权重乘法和实数FFT输出,并从结果中获得实部
综上DCT4处理可以用以下框图描述:

离散余弦变换 - IV型
- 算法:
- N-点 IV型 DCT 公式定义为实数线性转换:
其中
k = 0,1,2,.....N-1
- 它的逆运算定义为:
其中
n = 0,1,2,.....N-1
- DCT4矩阵通过乘以sqrt(2 / N)的总比例因子而变得对合(即它们是自逆的)。 变换矩阵的对称性说明用于正向和反向变换计算的快速算法是相同的。 注意,DCT4和逆DCT4的实现是相同的,因此,它们可以使用相同的处理函数。
- 转换支持的长度:
- 由于 DCT4 内部使用实数 FFT, 它支持所有 csky_rfft_f32() 支持的长度. 为Q15,Q31和浮点分别提供了不同的函数。
- 结构体实例
- 实数FFT和FFT的实例,余弦值表和旋转因子表都保存在一个数据结构的实例中。 每个转换都必须定义一个单独的数据结构体实例。 为支持的3种数据类型分别提供了不同的结构体实例。
- 初始化函数
- 每个不同的数据类型都有相应的初始化函数。 初始化函数处理以下操作:
- 是否使用初始化函数是可选的。 但是,使用了初始化函数,则不能将结构体实例放在常量数据段。 要将结构体实例放在常量数据段,则必须手动初始化结构体实例。 手动初始化结构体实例如下:
*csky_dct4_instance_f32 S = {N, Nby2, normalize, pTwiddle, pCosFactor, pRfft, pCfft};
*csky_dct4_instance_q31 S = {N, Nby2, normalize, pTwiddle, pCosFactor, pRfft, pCfft};
*csky_dct4_instance_q15 S = {N, Nby2, normalize, pTwiddle, pCosFactor, pRfft, pCfft};
其中 N 是DCT4的长度; Nby2 是DCT4长度的一半; normalize 是使用的归一化因子,并且相等于 sqrt(2/N); pTwiddle 指向旋转因子表; pCosFactor 指向余弦因子表; pRfft 指向实数FFT实例; pCfft 指向复数FFT实例; CFFT 和 RFFT 结构体也需要被初始化,详细情况参考负责初始化的 csky_rfft_f32() .
- 定点行为
- 使用定点DCT4转换函数需要注意。 特别是要考虑,在每个函数内使用的累加器的溢出和饱和行为。 具体参考每个函数各自的文档和使用说明。
- 参数
-
| [in] | *S | 指向浮点DCT/IDCT4结构体实例 |
| [in] | *pState | 指向状态缓存 |
| [in,out] | *pInlineBuffer | 指向原地输入和输出缓存 |
- 返回
- none.
- 参数
-
| [in,out] | *S | 指向浮点DCT4/IDCT4结构体实例 |
| [in] | *S_RFFT | 指向浮点RFFT/RIFFT结构体实例 |
| [in] | *S_CFFT | 指向浮点CFFT/CIFFT结构体实例 |
| [in] | N | DCT4的长度. |
| [in] | Nby2 | DCT4的长度的一半 |
| [in] | normalize | 归一化因子 |
- 返回
- csky_status 如果初始化成功,则函数返回 CSKY_MATH_SUCCESS ,如果
fftLenReal是不支持的变换长度,则返回 CSKY_MATH_ARGUMENT_ERROR
- 归一化因子:
- 归一化因子是
sqrt(2/N), 依赖于变换大小 N. 下表提供不同的DCT大小的浮点归一化因子:
| DCT大小 | 归一化因子的值 |
| 2048 | 0.03125 |
| 512 | 0.0625 |
| 128 | 0.125 |
- 参数
-
| [in,out] | *S | 指向 Q15 DCT4/IDCT4 结构体实例 |
| [in] | *S_RFFT | 指向 Q15 RFFT/RIFFT 结构体实例. |
| [in] | *S_CFFT | 指向 Q15 CFFT/CIFFT 结构体实例. |
| [in] | N | DCT4的长度. |
| [in] | Nby2 | DCT4长度的一半. |
| [in] | normalize | 归一化因子. |
- 返回
- csky_status 初始化成功,则函数返回 CSKY_MATH_SUCCESS,如果
N不是支持的变换长度,则返回 CSKY_MATH_ARGUMENT_ERROR
- 归一化因子:
- 归一化因子是
sqrt(2/N), 依赖于变换的大小 N. 归一化因子是 1.15 格式,下表罗列了在不同DCT大小的值:
| DCT大小 | 归一化因子的值(16进制) |
| 2048 | 0x400 |
| 512 | 0x800 |
| 128 | 0x1000 |
- 参数
-
| [in,out] | *S | 指向 Q31 DCT4/IDCT4 结构体实例. |
| [in] | *S_RFFT | 指向Q31 RFFT/RIFFT 结构体实例 |
| [in] | *S_CFFT | 指向Q31 CFFT/CIFFT 结构体实例 |
| [in] | N | DCT4长度 |
| [in] | Nby2 | DCT4长度的一半 |
| [in] | normalize | 归一化因子. |
- 返回
- csky_status 初始化成功,则函数返回 CSKY_MATH_SUCCESS,如果
N 不是支持的变换长度,则返回CSKY_MATH_ARGUMENT_ERROR
- 归一化因子:
- 归一化因子是
sqrt(2/N), 依赖于变换的长度 N. 归一化因子是 1.31 格式,下表中罗列了不同DCT大小的值:
| DCT大小 | 归一化因子的值(16进制) |
| 2048 | 0x4000000 |
| 512 | 0x8000000 |
| 128 | 0x10000000 |
- 参数
-
| [in] | *S | 指向Q15 DCT4结构体实例 |
| [in] | *pState | 指向状态缓存 |
| [in,out] | *pInlineBuffer | 指向原地输入输出缓存 |
- 返回
- none.
- 输入和输出格式:
- RFFT处理函数的内部输入会被缩放以防止溢出。 缩放的位数,依赖于变换的大小。 不同DCT大小的输入和输出的格式和位的数量,缩放位的数量在下表中:
| DCT大小 | 输入格式 | 输出格式 | 向上缩放的位数 |
| 2048 | 1.15 | 11.5 | 10 |
| 512 | 1.15 | 9.7 | 8 |
| 128 | 1.15 | 7.9 | 6 |
- 参数
-
| [in] | *S | 指向Q31 DCT4结构体实例 |
| [in] | *pState | 指向状态缓存 |
| [in,out] | *pInlineBuffer | 指向原地输入输出缓存 |
- 返回
- none.
- 输入和输出格式:
- 输入样本需要缩小1个位来防止在Q31 DCT处理中饱和。 因为从DCT2转换到DCT4涉及到一个减法。 RFFT处理函数的内部输入会被缩放以防止溢出。 缩放的位数,依赖于变换的大小。 不同DCT大小的输入输出格式和位的数量,缩放位的数量在下表中:
| DCT大小 | 输入格式 | 输出格式 | 向上缩放的位数 |
| 2048 | 2.30 | 12.20 | 11 |
| 512 | 2.30 | 10.22 | 9 |
| 128 | 2.30 | 8.24 | 7 |
- 余弦因子表的生成公式 :
cos_factors[n] = 2 * cos((2n+1)*pi/(4*N))
- 生成表的C代码
for(i = 0; i< N; i++)
{
cos_factors[i]= 2 * cos((2*i+1)*c/2);
}
- 其中
N 是要生成的权重的数量,c 是 pi/(2*N)
- 余弦因子表生成使用的公式 :
cos_factors[n] = 2 * cos((2n+1)*pi/(4*N))
- 生成表使用的c代码:
for(i = 0; i< N; i++)
{
cos_factors[i]= 2 * cos((2*i+1)*c/2);
}
- 其中
N 是需要生成的因子数量, c 是 pi/(2*N)
- 转换到Q15格式需要乘以 2^31 ,如果需要的话饱和.
| const q31_t cos_factorsQ31_128[128] |
|
static |
- 余弦因子表生成使用的公式 :
cos_factors[n] = 2 * cos((2n+1)*pi/(4*N))
- 表生成的C代码
for(i = 0; i< N; i++)
{
cos_factors[i]= 2 * cos((2*i+1)*c/2);
}
- 其中
N 是生成因子的数量, c 是 pi/(2*N)
- 转换到Q31格式需要乘以 2^31 ,并且在需要的时候饱和.
| const q31_t cos_factorsQ31_2048[2048] |
|
static |
| const q31_t cos_factorsQ31_512[512] |
|
static |
| const q31_t cos_factorsQ31_8192[8192] |
|
static |
- 权重表生成的公式 :
weights[n] = e^(-j*n*pi/(2*N))
- 生成表的C代码
for(i = 0; i< N; i++)
{
weights[2*i]= cos(i*c);
weights[(2*i)+1]= -sin(i * c);
}
- 其中
N 是要计算的权重的数量, c 是 pi/(2*N)
- 下表中,实部和虚部的值交错放置,因此数组的长度是
2*N.
- 权重表生成使用的公式 :
weights[n] = e^(-j*n*pi/(2*N))
- 生成表使用的C代码
for(i = 0; i< N; i++)
{
weights[2*i]= cos(i*c);
weights[(2*i)+1]= -sin(i * c);
}
- 其中
N 是需要计算的权重数量, c 是 pi/(2*N)
- 转换输出到Q15格式需要乘以 2^31 ,如果需要的话饱和.
- 下表中,实部和虚部值交错放置,因此数组的长度是
2*N.
| const q31_t WeightsQ31_128[256] |
|
static |
- 权重表生成使用的公式 :
weights[n] = e^(-j*n*pi/(2*N))
- 表生成使用的C代码
for(i = 0; i< N; i++)
{
weights[2*i]= cos(i*c);
weights[(2*i)+1]= -sin(i * c);
}
- 其中
N 是需要计算的权重数量, c 是 pi/(2*N)
- 转换输出到Q31格式,需要乘以 2^31,并且在需要的时候饱和.
- 下表中实部和虚部值交替排列,因此数组的长度是
2*N.
| const q31_t WeightsQ31_2048[4096] |
|
static |
| const q31_t WeightsQ31_512[1024] |
|
static |
| const q31_t WeightsQ31_8192[16384] |
|
static |