描述说明:

用复数FFT，复数和复数相乘以及支持函数演示卷积定理。

算法:

卷积定理说明时域中的卷积对应于频域中的乘法。 因此，两个信号的卷积的傅里叶变换等于它们各自的傅里叶变换的乘积。 可以使用快速傅里叶变换（FFT）来有效地评估信号的傅立叶变换。

两个输入信号, a[n] 和 b[n], 长度分别是 n1 和 n2 , 填充0让它们的长度为 N, 令其大于等于 (n1+n2-1) 并且是4的幂，因为FFT使用的是radix-4。 获取a[n] 和 b[n] 的卷积可以通过：两个输入信号的傅里叶变换相乘，然后逆向FFT相乘结果

可以表示为以下形式:

 A[k] = FFT(a[n],N)
B[k] = FFT(b[n],N)
conv(a[n], b[n]) = IFFT(A[k] * B[k], N)

其中 A[k] 和 B[k] 分别是N-点信号a[n] 和 b[n] 的FFT。 卷积信号的长度 (n1+n2-1).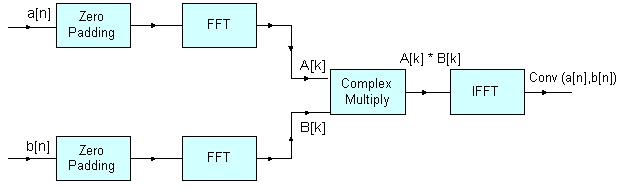

框图:

变量寿命:

• testInputA_f32 指向第一个输入序列
• srcALen 第一个输入序列的长度
• testInputB_f32 指向第二个输入序列
• srcBLen 第二个输入序列的长度
• outLen 卷积输出序列的长度, (srcALen + srcBLen - 1)
• AxB 指向保存输入信号分别生成的FFT输出的数组

CSI DSP 软件库函数使用了:

• csky_fill_f32()
• csky_copy_f32()
• csky_cfft_radix4_init_f32()
• csky_cfft_radix4_f32()
• csky_cmplx_mult_cmplx_f32()

参考 csky_convolution_example_f32.c